Convergence classes

BigDFT uses wavelets on a discretization grid to represent the wavefunction and density of the electronic system. The key parameters of a BigDFT calculation therefore are the grid spacing (noted hgrids) and the grid extension (noted rmult). The convergence of a given BigDFT calculation with respect to those two parameters can easily be studied via two classes: HgridsConvergence and RmultConvergence. Both will be used here in the case of the N\(_2\) molecule with the LDA exchange-correlation potential.

# Import the relevant modules, classes and constant.
import numpy as np
import matplotlib.pyplot as plt
from mybigdft import Posinp, Atom, InputParams, Job
from mybigdft.globals import EV_TO_HA

rmult convergence

The RmultConvergence class allows to run all the necessary calculations to determine the smallest grid extensions which must be used so that the energy error compared to the reference calculation (i.e., with the largest rmult considered) lie within the required precision per atom. Using the smallest rmult as possible allows to save computational time because there are less grid points (or degrees of freedom).

Note that there actually are two grids centered on the atoms of the system: a fine one with a shorter extension and a coarse one with a longer extension. They respectively correspond to the two numbers in the reference list given when initializing the RmultConvergence instance. These numbers will be decreased by 1 until the resulting energy lies outside the given precision_per_atom (here, 10 meV). The maximal number of jobs to be run is fixed to 6.

from mybigdft.workflows.convergences import RmultConvergence

atoms = [Atom('N', [0, 0, 0]), Atom('N', [0, 0, 1.1])]
pos = Posinp(atoms, units="angstroem", boundary_conditions="free")
base = Job(posinp=pos, run_dir="N2/rmult_convergence", name="N2")
rmc = RmultConvergence(base, reference=[9, 11], delta=[-1, -1], n_jobs=6,
                       precision_per_atom=0.01*EV_TO_HA)

The jobs in the queue have an extra attribute param which returns the value of rmult:

for job in rmc.queue:
    print(job.param)

[9.0, 11.0]
[8.0, 10.0]
[7.0, 9.0]
[6.0, 8.0]
[5.0, 7.0]
[4.0, 6.0]

You can run the calculations as usual:

rmc.run(nmpi=6, nomp=3)

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/rmult_convergence/9.0_11.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/rmult_convergence/8.0_10.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/rmult_convergence/7.0_9.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/rmult_convergence/6.0_8.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/rmult_convergence/5.0_7.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/rmult_convergence/4.0_6.0
Logfile log-N2.yaml already exists!

Once the calculations are performed, a converged job is determined. It corresponds to the one with the smallest rmult so that the total energy of the system is below the convergence threshold, defined by the sum of the energy found for the largest rmult and the user defined precision per atom. It can be accessed via the converged attribute:

rmc.converged.param

[5.0, 7.0]

The result of the previous cell shows that rmult = [5.0, 7.0] gives converged results for the given precision per atom. To make sure that everything ran as expected, all the relevant data can be accessed via the summary method:

rmc.summary()

Requested precision per atom: 3.67e-04 (Ha)
----------------------------------------------------
    rmult     precision_per_atom (Ha)  is_converged
----------------------------------------------------
 [9.0, 11.0]          0.00e+00             True
 [8.0, 10.0]          1.09e-06             True
  [7.0, 9.0]          3.71e-06             True
  [6.0, 8.0]          4.96e-06             True
  [5.0, 7.0]          2.75e-04             True
  [4.0, 6.0]          2.31e-03            False

Plotting the convergence

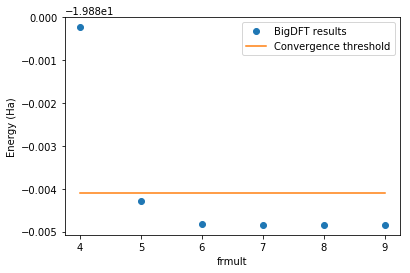
The figure below shows the convergence of the total energy of the N\(_2\) system with respect to the rmult. The threshold is also shown for comparison.

energies = [job.logfile.energy
            for job in rmc.queue if job.is_completed]
rmults = [job.param
          for job in rmc.queue if job.is_completed]
frmult = [rmult[0] for rmult in rmults]
n_at = len(rmc.queue[0].posinp)
threshold = min(energies) + n_at*rmc.precision_per_atom

fig=plt.figure()
fig.patch.set_facecolor('white')  # When dark background
plt.plot(frmult, energies,
         label="BigDFT results", marker="o", linestyle='')
plt.plot(frmult, [threshold]*len(energies),
         label="Convergence threshold")
plt.xlabel("frmult")
plt.ylabel("Energy (Ha)")
plt.legend()
plt.show()

Remember that there are actually two grids: one known as the fine grid, the other being the coarse one. The former is more expensive (from a computational point of view) than the latter, and should therefore have a smaller extension. One can perform a more refined rmult convergence by testing the convergence with respect to that fine grid extensions: this will be done after the convergence with respect to hgrids.

hgrids convergence

The HgridsConvergence class allows to run all the necessary calculations to determine the largest hgrids which must be used so that the energy error compared to the reference calculation (with the lowest hgrids considered) lie within the required precision per atom. Using the largest hgrids as possible allows to save computational time because there are less grid points (or degrees of freedom).

from mybigdft.workflows.convergences import HgridsConvergence

atoms = [Atom('N', [0, 0, 0]), Atom('N', [0, 0, 1.1])]
pos = Posinp(atoms, units="angstroem", boundary_conditions="free")
inp = InputParams({"dft": {"rmult": rmc.converged.param}})
run_dir = "N2/hgrids_convergence/rm_{:.1f}_{:.1f}".format(*rmc.converged.param)
base = Job(inputparams=inp, posinp=pos, run_dir=run_dir, name="N2")
hgc = HgridsConvergence(base, reference=0.24, delta=0.02,
                        precision_per_atom=0.01*EV_TO_HA)

The jobs in the queue have an extra attribute hgrids:

for job in hgc.queue:
    print(job.param)

[0.24, 0.24, 0.24]
[0.26, 0.26, 0.26]
[0.28, 0.28, 0.28]
[0.3, 0.3, 0.3]
[0.32, 0.32, 0.32]
[0.34, 0.34, 0.34]
[0.36, 0.36, 0.36]
[0.38, 0.38, 0.38]
[0.4, 0.4, 0.4]
[0.42, 0.42, 0.42]

You can run the calculations as usual:

hgc.run(nmpi=6, nomp=3)

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.24_0.24_0.24
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.26_0.26_0.26
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.28_0.28_0.28
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.30_0.30_0.30
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.32_0.32_0.32
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.34_0.34_0.34
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.36_0.36_0.36
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/0.38_0.38_0.38
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/mybigdft/workflows/workflow.py:114: UserWarning: Some jobs of the workflow were not run.
  UserWarning)

Note that not all calculations were run: this is because the job with hgrids = 0.38 gave an energy that was above the requested precision per atom.

Once the calculations are performed, a converged job is determined. It corresponds to the one with the largest hgrids so that the total energy of the system is below the convergence threshold. It can be accessed via the converged attribute. Its param attribute can in turns be accessed:

hgc.converged.param

[0.36, 0.36, 0.36]

The result of the previous cell shows that hgrids = 0.36 gives converged results for the given precision per atom. To make sure that everything ran as expected, all the relevant data can be accessed as follows:

hgc.summary()

Requested precision per atom: 3.67e-04 (Ha)
-----------------------------------------------------------
       hgrids        precision_per_atom (Ha)  is_converged
-----------------------------------------------------------
 [0.24, 0.24, 0.24]          0.00e+00             True
 [0.26, 0.26, 0.26]          3.89e-07             True
 [0.28, 0.28, 0.28]          2.63e-05             True
 [0.30, 0.30, 0.30]          4.53e-05             True
 [0.32, 0.32, 0.32]          1.23e-04             True
 [0.34, 0.34, 0.34]          1.88e-04             True
 [0.36, 0.36, 0.36]          3.46e-04             True
 [0.38, 0.38, 0.38]          5.86e-04            False

It shows that everything ran as expected: the calculation with hgrids = 0.36 has the largest hgrids while still having an energy below the requested threshold.

Plotting the convergence

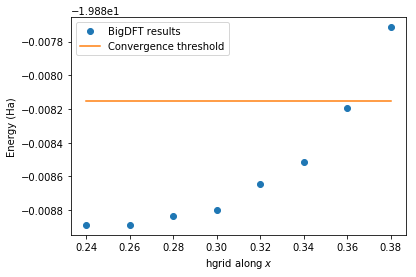
The figure below shows the convergence of the total energy of the N\(_2\) system with respect to hgrids. The threshold value is also shown for comparison.

energies = [job.logfile.energy
            for job in hgc.queue if job.is_completed]
hgrids = [job.param
          for job in hgc.queue if job.is_completed]
simple_hgrids = [hgrid[0] for hgrid in hgrids]
n_at = len(hgc.queue[0].posinp)
threshold = min(energies) + n_at*hgc.precision_per_atom

fig=plt.figure()
fig.patch.set_facecolor('white')  # When dark background
plt.plot(simple_hgrids, energies,
         label="BigDFT results", marker="o", linestyle='')
plt.plot(simple_hgrids, [threshold]*len(energies),
         label="Convergence threshold")
plt.xlabel("hgrid along $x$")
plt.ylabel("Energy (Ha)")
plt.legend()
plt.show()

frmult convergence

We started the convergence study with a coarse grid having a larger extension than the fine grid. This means that the coarse grid extension is converged, but there might still be some room to use a smaller fine grid. This is the reason why the convergence study ends by looking only at the fine grid extension multiplying factor frmult (note that the delta value for crmult is 0):

[frm, crm] = rmc.converged.param
frmc = RmultConvergence(base, reference=[frm+2, crm], delta=[-1, 0],
                        n_jobs=5, precision_per_atom=0.01*EV_TO_HA)

frmc.run(nmpi=6, nomp=3)

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/7.0_7.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/6.0_7.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/5.0_7.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/hgrids_convergence/rm_5.0_7.0/4.0_7.0
Logfile log-N2.yaml already exists!

/Users/maximemoriniere/Documents/Python/MyBigDFT/mybigdft/workflows/workflow.py:114: UserWarning: Some jobs of the workflow were not run.
  UserWarning)

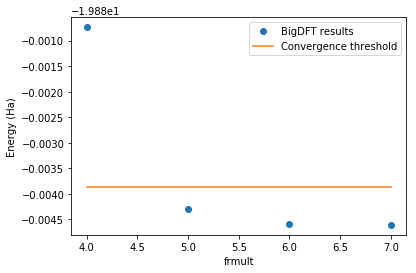
Nothing changed: frmult = 5.0 gives converged results for the given precision:

frmc.summary()

Requested precision per atom: 3.67e-04 (Ha)
---------------------------------------------------
   rmult     precision_per_atom (Ha)  is_converged
---------------------------------------------------
 [7.0, 7.0]          0.00e+00             True
 [6.0, 7.0]          1.17e-05             True
 [5.0, 7.0]          1.55e-04             True
 [4.0, 7.0]          1.93e-03            False

energies = [job.logfile.energy
            for job in frmc.queue if job.is_completed]
rmults = [job.param
          for job in frmc.queue if job.is_completed]
frmult = [rmult[0] for rmult in rmults]
n_at = len(frmc.queue[0].posinp)
threshold = min(energies) + n_at*frmc.precision_per_atom
fig=plt.figure()
fig.patch.set_facecolor('white')  # When dark background
plt.plot(frmult, energies,
         label="BigDFT results", marker="o", linestyle='')
plt.plot(frmult, [threshold]*len(energies),
         label="Convergence threshold")
plt.xlabel("frmult")
plt.ylabel("Energy (Ha)")
plt.legend()
plt.show()

Conclusion

The convergence with a precision per atom of 10 meV for the N\(_2\) molecule is found using hgrids = 0.36 and rmult = [5.0, 7.0] as input parameters for a BigDFT calculation.