Dissociation curve¶
MyBigDFT comes with some classes implementing particular workflows of calculations. These workflows define a queue of jobs, that can easily be run sequentially, without having to worry about the Job context manager. They also generally define a particular post-processing procedure, run after all the BigDFT calculations in order to extract some meaningful imformation.
The example provided here shows how to obtain the dissociation curve of the N\(_2\) molecule by using the Dissocation class.
Initialization¶
You first need to import some useful classes to define a ground state calculation as well as the Dissociation class, that is a workflow:
[1]:
import numpy as np
from mybigdft import Posinp, Atom, InputParams
from mybigdft.workflows import Dissociation
The Dissocation class¶
This class allows to compute the dissocation curve of two subsystems. To that end, you need to define two subsystems via Posinp instances (here, both subsystems are the same nitrogen atom) and a set of distances between those two subsystems. From these data, the Dissociation class defines a queue of jobs, that differ only by the initial positions: for each specified distance between both subsytem, the second fragment is translated by that amount along the \(y\) direction. This means
you could study the dissociation curve of two surfaces or of a molecule or of a single atom on top of that surface.
Of course, you can specify the input parameters you want to use for all these calculations, via the inputparams argument. You may also want to give a specific name to the runs and a specific folder where to run them, as usual.
[2]:
frag1 = Posinp([Atom('N', [0.0, 0.0, 0.0])], units="angstroem", boundary_conditions="free")
distances = np.arange(0.95, 1.25, 0.05)
inp = InputParams() # You might want to specify some non-default input parameters
dc = Dissociation(frag1, frag1, distances, inputparams=inp,
name="N2", run_dir="N2/dissociation_curve")
Running the workflow is done as usual:
[3]:
dc.run(nmpi=6, nomp=3)
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_0.95
Logfile log-N2.yaml already exists!
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.0
Logfile log-N2.yaml already exists!
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.05
Logfile log-N2.yaml already exists!
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.1
Logfile log-N2.yaml already exists!
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.1500000000000001
Logfile log-N2.yaml already exists!
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.2000000000000002
Logfile log-N2.yaml already exists!
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.2500000000000002
Logfile log-N2.yaml already exists!
You can check that the initial positions are as expected:
[4]:
for job in dc.queue:
print(job.run_dir, job.name)
print(job.posinp)
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_0.95 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 0.95 0.0
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.0 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 1.0 0.0
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.05 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 1.05 0.0
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.1 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 1.1 0.0
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.1500000000000001 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 1.15 0.0
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.2000000000000002 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 1.2 0.0
/Users/maximemoriniere/Documents/Python/MyBigDFT/doc/source/notebooks/N2/dissociation_curve/y_1.2500000000000002 N2
2 angstroem
free
N 0.0 0.0 0.0
N 0.0 1.25 0.0
The Dissociation class also has an energies attribute, storing the energy of each calculation. This is useful to plot the dissociation curve (see below).
[5]:
dc.energies
[5]:
[-19.805444659275025,
-19.85497382791818,
-19.878933352041976,
-19.884549270710195,
-19.877164837418295,
-19.86087438302971,
-19.838574516454937]
A more readable summary can be done as follows (thanks to the distance attribute of each job of the queue):
[6]:
for job in dc.queue:
print(f"d = {job.distance:.2f} {job.posinp.units}: {job.logfile.energy:.4f} Ha")
d = 0.95 angstroem: -19.8054 Ha
d = 1.00 angstroem: -19.8550 Ha
d = 1.05 angstroem: -19.8789 Ha
d = 1.10 angstroem: -19.8845 Ha
d = 1.15 angstroem: -19.8772 Ha
d = 1.20 angstroem: -19.8609 Ha
d = 1.25 angstroem: -19.8386 Ha
The job with the minimal energy is also stored under the minimum attribute:
[7]:
dc.minimum.distance, dc.minimum.logfile.energy
[7]:
(1.1, -19.884549270710195)
It is then easy to plot the actual dissociation curve:
[8]:
%matplotlib inline
import matplotlib.pyplot as plt
fig=plt.figure()
fig.patch.set_facecolor('white') # useful when dark background used on jupyter lab
plt.plot(dc.distances, dc.energies)
plt.xlabel("Distance [{}]".format(dc.queue[0].posinp.units))
plt.ylabel("Energy [Ha]")
plt.show()
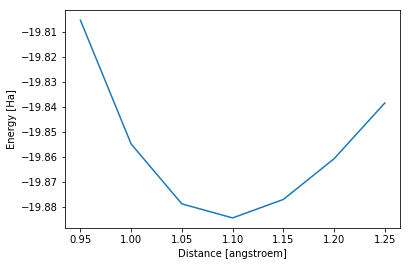
The results found here are as expected: when performing a geometry optimization of the N\(_2\) molecule, you actually get a distance of 1.0935 \(\unicode[serif]{xC5}^4\) with default input parameters.
Some errors are raised:¶
If periodic boundary conditions are used…
… because it is not possible to define a distance between two fragments under such boundary conditions.
[9]:
from copy import deepcopy
frag1 = Posinp([Atom('N', [0.0, 0.0, 0.0])], units="angstroem", boundary_conditions="free")
frag2 = deepcopy(frag1)
frag2._boundary_conditions = "periodic"
distances = np.arange(0.95, 1.25, 0.05)
dc3 = Dissociation(frag1, frag2, distances)
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
<ipython-input-9-4e208da571b1> in <module>()
4 frag2._boundary_conditions = "periodic"
5 distances = np.arange(0.95, 1.25, 0.05)
----> 6 dc3 = Dissociation(frag1, frag2, distances)
~/Documents/Python/MyBigDFT/mybigdft/workflows/dissociation.py in __init__(self, fragment1, fragment2, distances, inputparams, name, run_dir)
69 raise ValueError(
70 "Cannot compute a dissociation curve with periodic "
---> 71 "boundary conditions:\n{}".format(frag))
72 # Make sure both fragments use the same units (could actually be
73 # implemented properly in the __add__ method of posinp)
ValueError: Cannot compute a dissociation curve with periodic boundary conditions:
1 angstroem
periodic
N 0.0 0.0 0.0
If units differ…
… because the unit conversion is not yet implemented!
[10]:
from copy import deepcopy
frag1 = Posinp([Atom('N', [0.0, 0.0, 0.0])], units="angstroem", boundary_conditions="free")
frag2 = deepcopy(frag1)
frag2._units = "atomic"
distances = np.arange(0.95, 1.25, 0.05)
dc2 = Dissociation(frag1, frag2, distances)
---------------------------------------------------------------------------
NotImplementedError Traceback (most recent call last)
<ipython-input-10-072a4efcd7d5> in <module>()
4 frag2._units = "atomic"
5 distances = np.arange(0.95, 1.25, 0.05)
----> 6 dc2 = Dissociation(frag1, frag2, distances)
~/Documents/Python/MyBigDFT/mybigdft/workflows/dissociation.py in __init__(self, fragment1, fragment2, distances, inputparams, name, run_dir)
74 if fragment1.units != fragment2.units:
75 raise NotImplementedError(
---> 76 "Unit conversion of positions needed") # pragma: no cover
77 # Set the base attributes that are specific to this workflow
78 self.fragment1 = fragment1
NotImplementedError: Unit conversion of positions needed